知乎https://www.zhihu.com/people/kuingcry同步发布
大约半年前在csdn写了RSA算法的第一篇,鸽了半年多,现在终于把第二篇写出来了。。。
日常的基础应用,登录远程服务器
在使用ssh登录服务器的时候,每次都需要输入密码,为了解决这个问题,我们一般采取使用ssh-keygen命令在本地生成公钥和私钥两个文件,然后将公钥文件的内容追加到服务器家目录的./ssh文件夹中的authorized_keys文件里的方式来解决。
那么,到底什么是公钥,什么又是私钥,为何这一对"钥匙"可以代替密码来进行验证呢?
首先让我们来看一下在我们输入ssh命令登录服务器的过程中发生了什么:
- 客户端使用
ssh usrname@hostname命令向服务器发送了一个连接请求; - 在服务器接收到我们的信息后,会在authorized_keys文件里查找是否有对应的用户名信息,如果有的话就随机生产一个字符串,我们记作String_A;
- 服务器使用用户名对应的公钥进行加密,然后发送回客户端;
- 客户端用自己电脑上保存的和公钥对应的私钥对收到的加密后的信息进行处理,得到一串字符串String_B,然后发回给服务器;
- 服务器会对比String_A和String_B,如果相同,就认为客户端是可信的,免除密码进行登录。
可以发现,在整个流程中,实际上就是一套加密和解密的过程,公钥是一种加密方法,私钥是一种解密方法,而且这是一套非对称的加密方法。也就是说,我们的加密方法,也就是公钥是公开的,谁都可以获取,然后用来对要传输的信息进行加密,但是私钥是不公开的,只有创建公私钥的人才有。那为什么我们的加密方法都公开了,也不怕别人通过研究方法倒推出解密方法呢,就让我们来仔细研究一下这一对公私钥和加密算法。
公私钥文件
首先查看我们生成的公钥"id_rsa.pub"文件,内容如下:
ssh-rsa
AAAAB3NzaC1yc2EAAAADAQABAAABAQC3cPGQnTrUfzBbmfLUAfFrpfeu4s54xFcUTul+aFUiVg2fcVNJBIDaRjUpAJ03ZMJaz1N6bqe52Jg0Bd7FI/H72IZ3mqrSAedGaljV+vj/uVAZqaclJK541lBT4oAW3PO8lgwBd4vYj6PvyIb+9M5/Ro/HgwGqKfh1co/LWeRPGthuj3ZYbSJF0+JFiOuKi6Gdryj0xODGrtEjMVHdu9/YzDTUod9Wx5gOmzwk9Pyy5dc4PQk4rdf7ek8guFMw7LJjevT2HWdwqqQ8E5AjhdbDFo7QH9erI8w93u9bCE3X+fRvER4ykxb0MJ1UPQBPpcL7a7jGWQfyx1cYXSWNzw+n
XXXXXX@XXXXXX
可以看到第一行写明了我们的加密算法->大名鼎鼎的RSA加密算法,后面的是正式的秘钥内容,我们可以用base64 -d命令解码,然后hexdump -C命令标准十六进制和ascii码,结果如下所示: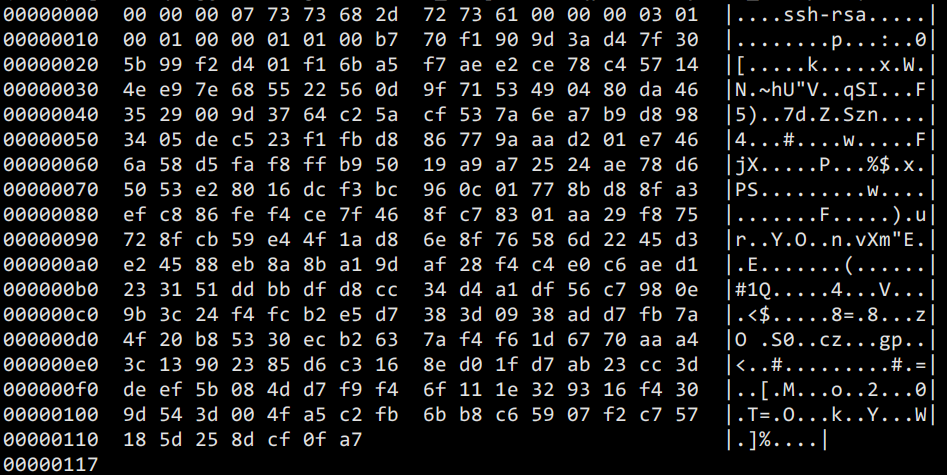
来逐行解读这段文件:
- 前4个字节 "00 00 00 07" 说明了接下来的数据块是7个字节长,接下来的7个字节的内容"73 73 68 2d 72 73 61", 每个字节用一个16进制数字表示,查ASCII表,正好对应了字符串 "ssh-rsa";
- 随后的4个字节"00 00 00 03"说明了接下来的数据块是3个字节长,接下来的3个字节的内容就是"01 00 01",使用
int('010001',16)换算成十进制是65537,这个数字我们用e来代表,在之后的原理介绍中会用到; - 在接下来的4个字节"00 00 01 01"说明了接下来的数据块是257个字节长,其中,开头的"00"代表这是一个正数,而后面的256个字节,也就是2048比特说明这代表了一个2048位的二进制数字。
私钥文件是私密的,不能随意公开,我们通过openssl命令查看私钥文件"id_rsa"的内容,发现里面有几个模块,分别是:
- modulus
- publicExponent
- privateExponent
- prime1
- prime2
- exponent1
- exponent2
- coefficient
通过对比公私钥,我们很容易发现私钥的modulus模块的内容和公钥里的那个2048位的数字是一样的,我们一般记作"N",而publicExponent的值就是"0x10001",和我们上面提到的数值e是一样的,后面的privateExponent,prime1和prime2我们分别用字母d、p和q代表,这就是我们加解密用到的所有信息,另外的exponent1和exponent2以及coefficient都是用来校验的,并不影响整个加解密的过程。
现在我们有了5个数字:N,e,d,p,q,假设我们要加密的信息是一个小于N的数字m(将信息使用ASCII编码或Unicode编码转化为一串数字,然后切割成短于N的一系列数字),加密后的信息是数字c,那么我们用到的加密和解密算法就分别是:
$$
\begin{Bmatrix}
m^e\ mod\ N = c\ (加密)
\end{Bmatrix}
$$
$$
\begin{Bmatrix}
c^d\ mod\ N = m\ (解密)
\end{Bmatrix}
$$
在这个加密和解密的过程中用到的数学原理和计算方法以及代码,将在后续文章中进行逐步的讲解。








Comments NOTHING